Supervised Learning

info

In this chapter you'll be introduced to:

• Supervised Learning: Understanding how to formulate supervised learning tasks and the components involved.
• Regression Problems: Focusing on regression where the target variable is continuous.
• Machine Learning Systems: The steps involved in building a machine learning model, including defining hypotheses and selection criteria.
• Hypothesis Class and Overfitting vs. Underfitting: Why specifying a hypothesis class is essential and the trade-offs in model complexity and their impact on performance.

What is Supervised Learning?

Supervised Learning is a type of machine learning where the model is trained using labeled data. The goal is to learn a function that maps inputs, $x$, to desired outputs, $y$, based on example input-output pairs. Our training dataset is a list of pairs $(x^{(i)}, y^{(i)})$, called training samples, where $i$ is the index into the training set. More precisely, we can define our training data consisting of $M$ examples:

$$\{ (\mathbf{x}^{(i)}, y^{(i)}) \}_{i=1}^M$$

• $\mathbf{x}^{(m)}$: Input vector for the $m$-th example.
• $y^{(m)}$: Target output for the $m$-th example.

Formulating a Supervised Learning Task

To formulate a supervised learning task, we need to:

• Define the Input Variables ($\mathbf{x}$): Features or attributes used to make predictions.
• Define the Target Variable ($y$): The outcome we want to predict.
• Specify the Task: For example, predicting the weight of an animal based on its size and fur texture.

Each task requires a specific target variable and input features. The formulation depends on the problem we aim to solve.

Input Features

The input in supervised learning is denoted as $\mathbf{x}$, a vector of features known during both training and prediction. These features can be:

• Real Numbers: Continuous values like size, weight, or temperature.
• Categorical Variables: Discrete categories like animal type or color.

If we have $d$ features, the input vector is:

$$\mathbf{x} = [x_1, x_2, \dots, x_d]^T$$

Handling Categorical Features

Categorical features cannot be directly used in mathematical models. We need to convert them into numerical representations.

One-Hot Encoding

One common method is one-hot encoding, where each category is represented by a binary vector.

• Example: Animal Type (Cat, Dog, Elephant)
  • Cat: [1, 0, 0]
  • Dog: [0, 1, 0]
  • Elephant: [0, 0, 1]

This avoids assigning arbitrary numerical values that could imply an unintended order or magnitude between categories.

We'll see other representations in latter chapters.

Output Targets

The target variable is denoted as $y$ (also denoted as $t$ in the literature). Depending on its nature, supervised learning tasks are classified as:

• Regression: If $y$ is a real number (continuous).
• Classification: If $y$ is a category from a finite set.

In these first few chapters, we'll focus on regression problems.

Regression Problems

In regression, the goal is to learn a function that maps input features to a continuous output. The regression model is denoted as $h$, where:

$$h: \mathbb{R}^d \rightarrow \mathbb{R}$$

• $d$: The number of input features.
• $h(\mathbf{x})$: The predicted output for input $\mathbf{x}$.

Given a new input $\mathbf{x}^*$, the model predicts the target as:

$$\hat{y} = h(\mathbf{x}^*)$$

Building a supervised learning model involves several steps:

1. Defining the Hypothesis Class

Humans define a set of possible models (functions) that the machine learning algorithm can choose from. This set is called the hypothesis class, denoted as $\mathcal{H}$.

$$\mathcal{H} \subseteq \{ h \mid h: \mathbb{R}^d \rightarrow \mathbb{R} \}$$

Why Specify a Hypothesis Class?

• Limiting the hypothesis class prevents the model from fitting noise in the training data, i.e., overfitting.
• Without restrictions, the model could choose any function, making learning from finite data impossible.

Overfitting

When a model is too complex, it fits the training data very well but performs poorly on new data.

• Cause: Hypothesis class is too powerful (too many functions).

Underfitting

When a model is too simple, it cannot capture the underlying pattern of the data.

• Cause: Hypothesis class is too limited.

In this step, we need to find a balance where the model is complex enough to capture the data patterns but simple enough to generalize well.

Example

In this example we show how a polynomial function would fit to data with different degrees of freedom. If the class is too strict (on the left) the function underfits the data. If the class is too powerful (on the right) the function overfits.

A Comparison underfitting, balanced fitting and overfitting from left to right¹.

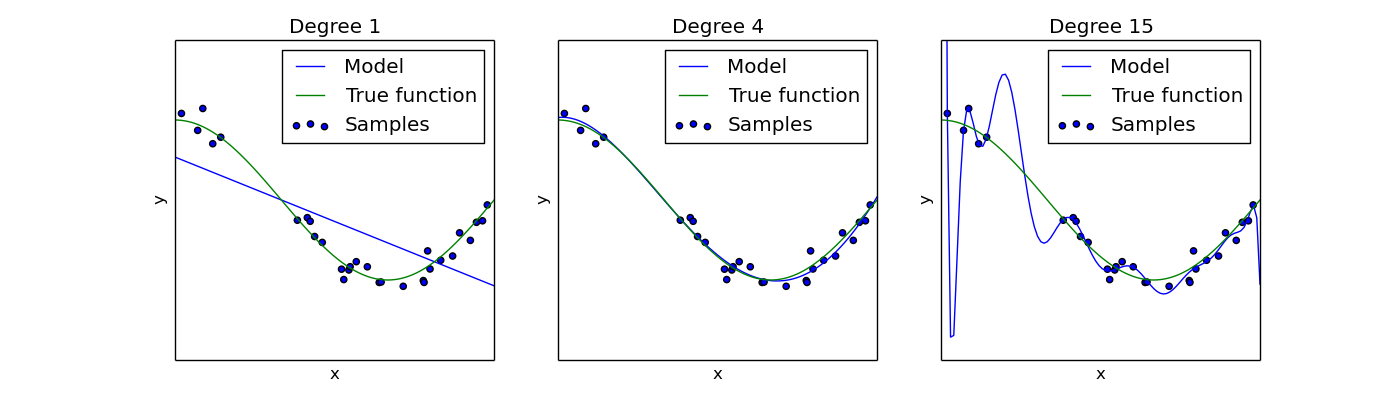
2. Defining the Selection Criterion

Humans specify a selection criterion (objective function) that evaluates how well a model fits the training data. Denoted as $J$, it's a function of the hypothesis $h$ and the training data.

$$J(h) = \text{Evaluation of } h \text{ on training data}$$

Our goal is to find the hypothesis $h$ that minimizes $J(h)$.

3. Training the Model

The machine learning algorithm selects the best hypothesis from $\mathcal{H}$ by minimizing the selection criterion:

$$h^* = \arg\min_{h \in \mathcal{H}} J(h)$$

4. Making Predictions

With the trained model $h^*$, predictions are made on new, unseen data $\mathbf{x}$:

$$\hat{y} = h^*(\mathbf{x})$$

5. Evaluating the Model

The model's performance is evaluated using a measure of success or error function $E(h)$ on unseen data:

$$E(h) = \text{Evaluation of } h \text{ on unseen data}$$

The objective is to assess how well the model generalizes to new data.

• Note: $E(h)$ is often different from the training criterion $J(h)$.

Recap

1. What is the primary goal of supervised learning?

• To cluster data points into groups
• To simulate decision-making through rewards
• To learn from unlabeled data
• To learn a mapping from inputs to outputs using labeled data

2. What does the training dataset in supervised learning consist of?

• Predictions and their errors
• Pairs of input vectors and corresponding target outputs
• Unlabeled data only
• A set of random features

3. In regression problems, what does the model predict?

• A binary decision
• A categorical label
• A sequence of actions
• A continuous output

4. What is the hypothesis class in a supervised learning model?

• A type of data preprocessing method
• The measure of error on unseen data
• The collection of input features
• A set of potential models (functions) from which the algorithm selects

5. Why is defining a hypothesis class important in supervised learning?

• It automatically generates training data
• It eliminates the need for evaluating model performance
• It helps prevent overfitting by limiting the complexity of models
• It ensures the model always predicts perfectly

What's Next

In the next chapter, we'll go through Linear Regression, a fundamental learning algorithm in supervised learning.

---

Footnotes

1. Portions of this page are reproduced from work created and shared by Scikit-learn and used according to terms described in the BSD 3-Clause License. ↩